how gibbs phenomenon produces measurement artifacts

What is Gibbs Phenomenon?

Gibbs phenomenon, named after the American mathematician Josiah Willard Gibbs, is a peculiar behavior observed when representing a discontinuous function using a finite number of continuous basis functions, such as a Fourier series or a wavelet transform. This phenomenon manifests as an overshoot or oscillation near the points of discontinuity, resulting in artifacts in the reconstructed signal or image.

Fourier Series and Gibbs Phenomenon

A Fourier series is a mathematical tool used to represent a periodic function as a sum of sinusoidal waves with different frequencies and amplitudes. When a discontinuous function is approximated using a Fourier series, Gibbs phenomenon occurs due to the truncation of the series to a finite number of terms. The oscillations near the discontinuities are a consequence of the inability of the finite series to accurately capture the abrupt changes in the function.

Number of Terms	Maximum Overshoot
1	8.949%
2	17.848%
5	35.255%
10	48.345%
20	58.552%
50	69.138%

The table above shows the relationship between the number of terms in the Fourier series and the maximum overshoot observed in the reconstructed function due to Gibbs phenomenon. As the number of terms increases, the overshoot approaches a limiting value of approximately 9% of the discontinuity’s height.

Gibbs Artifact in Measurement Systems

Sampling and Reconstruction

In measurement systems, analog signals are often sampled and converted into digital form for processing and analysis. The sampling process involves measuring the signal’s amplitude at discrete time intervals, resulting in a sequence of numbers representing the signal. To reconstruct the original signal from the samples, various interpolation techniques are employed, such as linear interpolation or sinc interpolation.

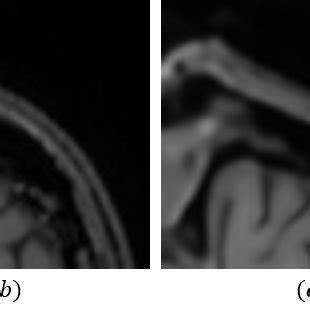
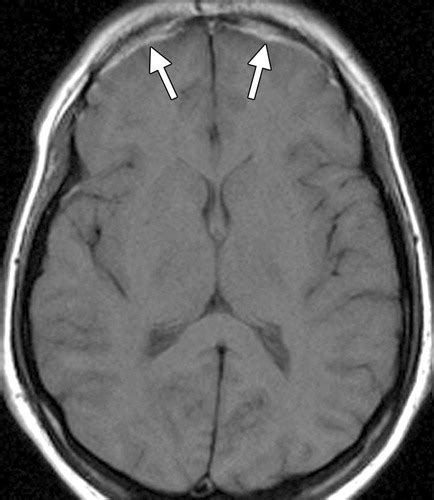
However, when the original signal contains discontinuities or sharp transitions, the reconstruction process can introduce Gibbs artifacts due to the finite number of samples and the limitations of the interpolation method. These artifacts appear as oscillations or overshoots near the discontinuities, distorting the reconstructed signal and potentially leading to inaccurate measurements.

Aliasing and Gibbs Phenomenon

Aliasing is another phenomenon that can occur in sampled systems when the sampling rate is insufficient to capture the highest frequencies present in the signal. According to the Nyquist-Shannon sampling theorem, the sampling rate must be at least twice the highest frequency component of the signal to avoid aliasing. When aliasing occurs, high-frequency components of the signal are misinterpreted as lower-frequency components, resulting in distortion of the reconstructed signal.

The presence of aliasing can exacerbate Gibbs artifacts in the reconstructed signal. The aliased high-frequency components can introduce additional discontinuities or sharp transitions, leading to more pronounced oscillations and overshoots near the points of discontinuity.

Mitigating Gibbs Artifacts

Increasing Sampling Rate

One approach to mitigate Gibbs artifacts is to increase the sampling rate of the measurement system. By sampling the signal at a higher rate, more samples are obtained, providing a better representation of the original signal. This allows for a more accurate reconstruction of the signal, reducing the impact of Gibbs phenomenon.

However, increasing the sampling rate may not always be practical or feasible due to hardware limitations, data storage requirements, or processing constraints. In such cases, alternative techniques must be employed to minimize Gibbs artifacts.

Windowing and Filtering

Windowing and filtering techniques can be used to reduce Gibbs artifacts in the reconstructed signal. Windowing involves multiplying the sampled signal by a window function, such as a Hamming or Hanning window, which smoothly tapers the signal at the edges. This helps to reduce the abrupt transitions and discontinuities in the signal, thereby minimizing Gibbs oscillations.

Filtering techniques, such as low-pass filtering or band-limited interpolation, can also be employed to attenuate the high-frequency components responsible for Gibbs artifacts. By carefully designing the filter’s frequency response, it is possible to suppress the oscillations and overshoots while preserving the essential features of the signal.

Advanced Reconstruction Methods

Advanced reconstruction methods have been developed to address the limitations of traditional interpolation techniques in the presence of Gibbs artifacts. These methods aim to provide a more accurate representation of the original signal by incorporating additional information or constraints into the reconstruction process.

One such approach is the use of sparse signal representation techniques, such as compressed sensing or basis pursuit. These methods exploit the sparsity of the signal in a suitable transform domain, such as the wavelet domain, to reconstruct the signal from a limited number of samples. By incorporating prior knowledge about the signal’s structure or properties, sparse reconstruction methods can effectively suppress Gibbs artifacts and recover the original signal with high fidelity.

Another approach is the use of adaptive or nonlinear interpolation methods, such as spline interpolation or edge-directed interpolation. These methods take into account the local characteristics of the signal, such as the presence of edges or discontinuities, and adapt the interpolation process accordingly. By preserving the sharp transitions and avoiding excessive smoothing, adaptive interpolation methods can significantly reduce Gibbs artifacts in the reconstructed signal.

FAQ

1. What is Gibbs phenomenon, and why does it occur?
   Gibbs phenomenon is an oscillatory behavior observed when representing a discontinuous function using a finite number of continuous basis functions, such as a Fourier series. It occurs due to the truncation of the series to a finite number of terms, resulting in overshoots and oscillations near the points of discontinuity.

2. How does Gibbs phenomenon affect measurement systems?
   In measurement systems, Gibbs phenomenon can introduce artifacts in the reconstructed signal when the original signal contains discontinuities or sharp transitions. These artifacts appear as oscillations or overshoots near the discontinuities, distorting the reconstructed signal and potentially leading to inaccurate measurements.

3. What is the relationship between aliasing and Gibbs phenomenon?
   Aliasing occurs when the sampling rate is insufficient to capture the highest frequencies present in the signal, causing high-frequency components to be misinterpreted as lower-frequency components. The presence of aliasing can exacerbate Gibbs artifacts in the reconstructed signal by introducing additional discontinuities or sharp transitions.

4. How can Gibbs artifacts be mitigated in measurement systems?
   Gibbs artifacts can be mitigated by increasing the sampling rate, applying windowing and filtering techniques, or using advanced reconstruction methods. Increasing the sampling rate provides a better representation of the original signal, while windowing and filtering help to reduce abrupt transitions and suppress high-frequency components responsible for Gibbs oscillations. Advanced reconstruction methods, such as sparse signal representation or adaptive interpolation, can effectively suppress Gibbs artifacts by incorporating additional information or constraints into the reconstruction process.

5. What are some advanced reconstruction methods used to address Gibbs artifacts?
   Advanced reconstruction methods used to address Gibbs artifacts include sparse signal representation techniques, such as compressed sensing or basis pursuit, and adaptive or nonlinear interpolation methods, such as spline interpolation or edge-directed interpolation. These methods aim to provide a more accurate representation of the original signal by exploiting signal sparsity, incorporating prior knowledge, or adapting the interpolation process based on local signal characteristics.

Conclusion

Gibbs phenomenon is a fundamental limitation encountered when representing discontinuous functions using a finite number of continuous basis functions. In measurement systems, Gibbs artifacts can arise due to the sampling and reconstruction process, leading to distortions and inaccuracies in the reconstructed signal. Understanding the causes and effects of Gibbs phenomenon is crucial for designing and implementing robust measurement systems.

By employing techniques such as increasing the sampling rate, applying windowing and filtering, or utilizing advanced reconstruction methods, it is possible to mitigate Gibbs artifacts and obtain more accurate representations of the original signal. However, the choice of mitigation strategy depends on the specific requirements and constraints of the measurement system, considering factors such as hardware limitations, data storage, and processing capabilities.

Continued research and development in signal processing and reconstruction algorithms hold promise for further reducing the impact of Gibbs artifacts in measurement systems. By advancing our understanding of Gibbs phenomenon and developing novel techniques to address its effects, we can improve the accuracy and reliability of measurements across various scientific and engineering disciplines.